Teorema de Lamy

Si un cuerpo rígido en equilibrio se encuentra sometido a la acción de tres (3) fuerzas, estas deben ser coplanares y sus líneas de acción deben ser concurrentes.

La razón por la que las tres fuerzas deben ser coplanares es bastante simple. Si no fuese así, no se cumpliría la primera condición de equilibrio.

Por ejemplo consideremos que un cuerpo se encuentra en equilibrio sometido a la acción de tres fuerzas no coplanares (ver figura superior). Como la resultante de dos de ellas no se anula con la tercera fuerza no se cumplirá la primera condición de equilibrio.

La razón por la que las tres fuerzas deben ser concurrentes también es bastante simple. Si no fuese así, no se cumpliría la segunda condición de equilibrio.

Por ejemplo analicemos el equilibrio de una barra que se encuentra suspendida de dos cuerdas oblícuas y supongamos que las líneas de acción de las tres fuerzas que actúan sobre ella no son concurrentes (ver figura). Si tomamos momentos respecto del punto en donde convergen dos de ellas, habría un torque resultante provocada por la tercera fuerza que haría rotar a la barra, lo que hace que no se cumpla la segunda condición de equilibrio.

El teorema de Lamy, que fue enunciado por el religioso francés Bernard Lami (1645-1716), dice lo siguiente:

Cuando un cuerpo rígido en equilibrio se encuentra sometido a la acción de tres fuerzas concurrentes, el módulo de cada una es directamente proporcional al seno de su respectivo ángulo opuesto.

Este teorema es una consecuencia de la ley de senos aplicado luego de formar el triangulo de fuerzas.

De esto se deduce el siguiente lema:

Si un cuerpo se encuentra en equilibrio se encuentra sometido a la acción de tres (3) fuerzas, y los ángulos que forman entre si cada par de estas son iguales a 120^o, los módulos de estas fuerzas deben ser iguales.

PROBLEMA
Si el sistema mostrado en la figura se encuentra en equilibrio estático en la forma que se indica, y el bloque P pesa 21 N, determinar el peso del bloque Q.

Hagamos el DCL del nudo A, teniendo presente que la tensión de la cuerda que sostiene el bloque P es igual a su peso, y apliquemos el teorema de Lami:

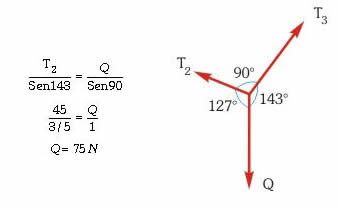
A continuación hagamos el DCL del nudo B, teniendo presente que la tensión de la cuerda que sostiene el bloque Q es igual a su peso, y apliquemos nuevamente el teorema de Lami: