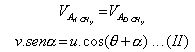Otro interesante problema adaptado de la OAF 2009, planteado en nuestro medio por nuestro amigo el profesor Douglas Ameida de São Paulo-Brasil y resuelto magistralmente por su compatriota Lucas Lugão Guimarães de Belo Horizonte.
Dos esferas que caen libremente y luego chocan con el piso
Una esfera A, de masa mucho menor que otra B, se encuentra apoyada sobre esta, formando un ángulo α, respecto a la vertical. Ambas se encuentran inicialmente a una altura h = 2 m, en un lugar donde la resistencia del aire es despreciable, como se muestra en la figura.
Luego que estas son liberadas, caen verticalmente hasta que B choca elásticamente con el piso, e inmediatamente después choca elásticamente con A que es lanzada oblicuamente llegando al suelo a la distancia horizontal L. Asumiendo que en el momento que B choca con el piso, A se encuentra alejado una distancia infinitesimal de A, que durante la colisión el rozamiento entre las esferas es despreciable y que los radios de las esferas son mucho más pequeños que h y L, determine el valor máximo valor de L.
Resolución
Como la esfera B efectúa un choque elástico con el piso, después del choque, que dura una fracción de segundo, este se moverá verticalmente con la misma rapidez que tenía antes del choque, la cual hemos denominado v. El valor de v se determina muy fácilmente por las ecuaciones del movimiento de caída libre, o aplicando el principio de conservación de la energía mecánica (v = √2gh).
De la condición del problema se deduce que en el instante que B se despega del piso, este efectúa un segundo choque (también elástico) con A que tenía prácticamente la misma rapidez v.
Analicemos detenidamente este segundo choque, suponiendo que las velocidades de A y B, después de este segundo choque son u y w respectivamente.
Como el choque es elástico (e = 1), la rapidez relativa entre A y B en la dirección normal a la superficie de choque (eje x) será la misma antes y después del choque.
Por otro lado, si bien el sistema formado por las dos esferas después del primer choque NO ES UN SISTEMA AISLADO, debido a la acción de la fuerza de gravedad, se puede considerar que se conserva su cantidad de movimiento, en el breve intervalo de tiempo que dura el choque, ya que el impulso generado por esta fuerza, en este intervalo de tiempo, es despreciable.
Apliquemos el principio de conservación de la cantidad de movimiento, del sistema formado por las dos esferas, en la dirección x, considerando que las masas de las esferas A y B son m y M respectivamente.
Reemplazando (1) en (2) y despejando se tiene que:
De esta expresión se deduce que, si la masa m es mucho menor que M, el término m/M puede despreciarse. De aquí se concluye que:
Por otro lado, como entre las esferas no existe rozamiento, la componente de la velocidad de A en el eje y, antes y después del choque, no cambiará. Según esto.
De estas ecuaciones se deduce, elevando al cuadrado ambos miembros y sumándolos miembro a miembro para eliminar el arco compuesto θ + ε, que:
De estas mismas ecuaciones (I) y (II) se deduce, dividiéndolas miembro a miembro, una relación entre los ángulos θ y α (tan(θ + α) = 3.cotα). A partir de esto obtengamos θ en función de α:
Finalmente, como una de las condiciones del problema es que las dimensiones de las esferas son despreciables respecto de las distancias h y L, se concluye que lo que nos piden determinar es el máximo alcance horizontal que puede alcanzar la esfera A durante su movimiento parabólico después de producido el segundo choque.
Recordemos que de las ecuaciones del movimiento parabólico se deduce que:
Por otro lado, recordando por trigonometría que:
reemplazando en esta ecuación el valor de la tangente (tanθ) obtenido anteriormente, se deduce que:
Reemplazando esta última expresión y la ecuación Σ en la ecuación del alcance horizontal, se deduce que:
Ahora el problema consiste en maximizar el valor del alcance horizontal L. Para maximizar el valor de L, que equivale a maximizar el valor de la expresión E = sen2α + sen4α, utilizaremos el criterio de la derivada.
De donde, resolviendo por la fórmula general para ecuaciones de segundo grado.
Y esto implica que α = 26,8o.
Reemplazando este valor en la ecuación del alcance horizontal L, teniendo en cuenta que v2 = 2gh = 40 m2/s2, se concluye que Lmax = 28,16 m aproximadamente.
Para acabar, quiero expresar un agradecimiento especial (una vez más) al maestro de maestros, Enrique Romero Osorio, que me ayudo a salir del intringulis matemático que me encontraba al resolver este problema.
Descargue la versión de Lucas Lugão (en portugués) desde aqui.