Un cuerpo se encuentra en equilibrio de traslación, si la fuerza resultante de todas las fuerzas externas que actúan sobre él es nulo.
Matemáticamente:
Para el caso de fuerzas coplanares que se encuentran en el plano cartesiano xy se reduce la fuerza resultante en cada uno de los ejes x e y es cero:

Geométricamente esto implica que estas fuerzas, al ser gráficadas una a continuación de la otra, de modo tal que el extremo de cada una coincida con el origen de otra, formen un polígono cerrado.

Para el caso particular que sobre el cuerpo actúan solo tres fuerzas, estas deben formar un triángulo de fuerzas.

PROBLEMA
El bloque mostrado tiene una masa m = 5 kg y se encuentra en equilibrio. Si el resorte (K = 20 N/cm) se encuentra estirado 4 cm, determinar la tensión de la cuerda vertical.
Como K = 20 N/cm, cuya interpretación es que por cada centímetro de deformación del resorte la fuerza elástica que se genera internamente es de 20 N, se deduce (ley de Hooke) que cuando la deformación sea de 4 cm la fuerza elástica en el resorte será de 80 N.
Hagamos DCL del bloque, teniendo presente que tanto el resorte como la cuerda vertical se encuentran "tensadas" y por tanto las fuerzas que actúan sobre el bloque debido a estos cuerpos se grafican "saliendo" del bloque, y apliquemos la 1ra condición de equilibrio.

PROBLEMA
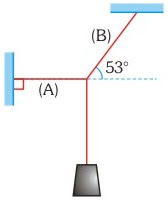
Si el bloque mostrado en las figura pesa 120 N, determinar las tensiones de las cuerdas A y B.
Como sobre el bloque solo actúan dos fuerzas (la fuerza de la gravedad y la tensión de la cuerda vertical) y este se encuentra en equilibrio, la tensión de la cuerda será igual (en módulo) a la fuerza de la gravedad del bloque.
A continuación hagamos DCL del nudo en donde convergen las tres cuerdas, teniendo presente que las tensiones de las tres cuerdas "salen" del nudo, y a continuación construyamos el triángulo de fuerzas.

Lo que a continuación se tiene que hacer es resolver, el triángulo de fuerzas construido. En este caso, relacionando el triángulo de fuerzas con el triángulo notable de 37° y 53°, deducimos que (k = 30).

PROBLEMA
Si la esfera mostrada en la figura es de 20N, y el módulo de la fuerza F aplicada es de 80 N, determinar los módulos de las reacciones del apoyo en A y B.
Hagamos DCL de la esfera teniendo presente que las reacciones del apoyo en A y B son perpendiculares a las superficies en contacto y se grafican "entrando" al cuerpo que se analiza.

Teniendo presente que los ángulos de la dos perpendiculares son iguales, deducimos que la reacción del apoyo en A (RA) forma con la vertical un ángulo que es igual al ángulo diedro 2θ.
Por otro lado, tenido presente que los ángulos alternos internos entre rectas paralelas son iguales, deducimos que la fuerza F forma con la horizontal un ángulo θ.
A continuación construyamos el triángulo de fuerzas tenido presente que la resultante de la reacción del apoyo en B y el peso apunta hacia arriba.

Se comprueba que el triángulo de fuerzas es un triángulo equilátero y por tanto:





0 comentarios:
Publicar un comentario