Otro problema interesante propuesto por uno de los miembros de nuestra Sociedad Peruana de Docentes de Física.
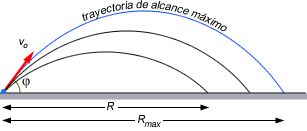
Alcance máximo de un un chorro de agua en un tubería
Una boquilla, ubicada en el extremo inferior A de una tubería cilíndrica de diámetro d = 1 m y pendiente 1%, descarga sobre el interior de esta tubería un chorro de agua con una velocidad vo = 10 m/s. Determine el máxima distancia R que puede alcanzar este chorro de agua, a lo largo de la tubería. Considere g = 10 m/s2.
Resolución
Es un hecho conocido cuando el ángulo φ con que se lanza un proyectil desde la superficie de la tierra va aumentando, comenzando desde un valor pequeño, el alcance horizontal R también aumenta hasta alcanzar un valor máximo que se da cuando φ = 45o.
En este proceso, cuando el ángulo de lanzamiento φ aumenta de 0 a 45o, la altura máxima alcanzada por el proyectil también aumenta.
Pero en el problema propuesto nos piden el alcance máximo R con la limitante que existe una altura máxima que puede alcanzar el chorro de agua (no debe chocar con las paredes de la tubería).
Pero en el problema propuesto nos piden el alcance máximo R con la limitante que existe una altura máxima que puede alcanzar el chorro de agua (no debe chocar con las paredes de la tubería).
De este razonamiento deducimos que el alcance R será máximo cuando el chorro de agua roce la pared interna superior de la tubería.
En este problema la pendiente de la tubería es del 1% (tanθ = 0,01) lo que indica que el eje de la tubería se encuentra ligeramente inclinada.
Para resolver este problema, por criterios académicos, asumiremos gráficamente que la tubería se encuentra notoriamente inclinada y lo primero que haremos es tomar un sistema de coordenadas xy ubicado en un plano vertical, donde el eje x sea paralelo al eje de la tubería.
Descompongamos la velocidad inicial de lanzamiento v y la gravedad g en componentes rectangulares a lo largo de dichos ejes coordenados y analizaremos cada uno de los movimientos componentes (ambos son MRUA).
Vamos a plantear las ecuaciones, considerando que como el ángulo θ es pequeño las funciones seno y coseno de dicho ángulo son aproximadamente 0 y 1 respectivamente.
Primero, determinemos el tiempo que una partícula de agua tarda en recorrer el tramo BC (que es igual al que tarda en recorrer el tramo AB), teniendo en cuenta que la velocidad inicial del movimiento componente a lo largo del eje y, en este tramo, es nula.
A continuación, determinemos el ángulo ε que forma la velocidad de lanzamiento con el eje x teniendo en cuenta que la velocidad final del movimiento componente a lo largo del eje y, en el tramo AB, es nula.
Reemplazando en esta ecuación el tiempo t calculado en el paso anterior, y aproximando cosθ a uno, concluimos que:
Finalmente, determinaremos el alcance horizontal R (máximo) teniendo en cuenta que el movimiento componente a lo largo del eje x, en el tramo AC, se da en un tiempo 2t y que senθ es aproximadamente igual a cero.