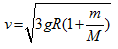Un interesante problema que se propuso en la Sociedad Peruana de Docentes de Física (conocida coloquialmente como la "sopa de fideos" por sus siglas en español SPDF) es el siguiente.
Máxima altura alcanzado por una de las parte de un sistema
La figura muestra el instante en que una canica de masa m hace su ingreso en una canaleta semicircular practicado en un coche de masa M que se encuentra inicialmente en reposo. Si despreciamos toda clase de rozamiento ¿cuál es el valor de la rapidez v para que la canica alcance una altura h = R/2 respecto de OA?
Resolución
Primeramente debemos señalar que cuando la canica se encuentra dentro de la canaleta, el coche experimentará una aceleración horizontal variable hasta el instante que la canica sale de ella. Después de esto la canica experimentará un movimiento parabólico de caída libre, y el coche un movimiento rectilíneo uniforme, ambos con una misma velocidad horizontal u, ya que a partir del instante en que la canica se libera del coche sobre ellos no actúa ninguna fuerza externa horizontal.
Como sobre el sistema no actúa ninguna fuerza externa horizontal, la cantidad de movimiento horizontal del sistema se conservará en el tiempo.
Por otro lado, como sobre el sistema se encuentra libre de toda fuerza de rozamiento (interna y externa), se conservará su energía mecánica. Tomando como estado inicial el instante en que la canica ingresa a la canaleta y estado final el instante en que la canica alcanza su máxima altura tenemos:
Reemplazando (1) en (2) y despejando tenemos: