sábado, 24 de abril de 2010
miércoles, 21 de abril de 2010
Teoría Cinética de Gases
La teoría cinética de gases explica las características macroscópicas de los gases (presión, temperatura, energía interna, etc) considerando que los gases están compuestos de una cantidad enorme de partículas (del orden 1023) que se encuentran en continuo movimiento caótico.
Los postulados básicos en que se basa esta teoría son que las colisiones que se producen entre las partículas con las paredes del recipiente son perfectamente elásticas, que los choques entre ellas son poco frecuentes, y que sus velocidades están distribuidas al azar, pero debido a la enorme cantidad de partículas que existe, hay igual probabilidad que una partícula se mueva longitudinalmente, lateralmente o verticalmente.
Este último postulado implica matemáticamente que los valores medios de sus velocidades cuadráticas en cada uno de los ejes cartesianos son iguales (en lenguaje matemático: < v2x> = < v2y> = < v2z>), y como el cuadrado del módulo de la velocidad de una partícula es v2 = v2x + v2y + v2z, se concluye que < v2> = 3 < v2x>.
La presión ejercida por el gas
Consideremos un recipiente cúbico que contiene un gas y analicemos el movimiento de una de sus partículas. Asumiendo que esta partícula choca elásticamente con una de sus paredes, y que durante su movimiento no choca con otra, determinemos la fuerza media <Fx> que se genera entre dos choques consecutivos.
De acuerdo con el teorema del impulso y la cantidad de movimiento tenemos que <Fx>.Δt = Δ(m.vx) = 2m.vx, pero como el tiempo entre dos choques consecutivos es Δt = 2L/vx, se deduce que la fuerza media generada entre una de las caras del recipiente y la partícula es <Fx> = m.v2x/L.
Si ahora consideramos que existen N partículas en el recipiente y que < v2x> = < v2>/3, la fuerza media generada sobre una de las paredes del recipiente será <Fx> = N.m.<v2>/3L, y por tanto la presión generada será: P = N.m.<v2>/3V, donde V es el volumen del recipiente.


De esta relación se aprecia que la presión ejercida por un gas sobre cada una de las paredes del recipiente que lo contiene es directamente proporcional a su densidad y al valor medio de la velocidad cuadrática de sus partículas.
Definición cinética de la temperatura
La temperatura de un sistema termodinámico es una variable que se mide indirectamente en función de los cambios observados en las propiedades macroscópicas del sistema cuando cambia la temperatura.
La ecuación de estado de un gas ideal relaciona las propiedades macroscópicas, presión P, el volumen V y temperatura T: PV = nRT. Combinando esta ecuación con la ecuación de la presión obtenida anteriormente, tenemos que:

En el primer miembro de esta ecuación se encuentra el valor medio de la energía cinética molecular <EK> y en el segundo miembro el cociente del número de moléculas N y el número de moles n del gas es el número de Avogadro No.
El cociente de la constante universal de los gases R y el número de Avogadro No, es otra constante denominada constante de Boltzmann designada con la letra k:
Finalmente tenemos que:
De esta relación se aprecia que el valor medio de la energía cinética molecular de un gas es directamente proporcional a su temperatura absoluta.
martes, 20 de abril de 2010
Teorema de Impulso y la Cantidad de Movimiento
Las tres Leyes de Newton, junto con las transformaciones de Galileo, son la base de la mecánica clásica.
Esta es la manera como se Newton enunció originalmente su segunda ley:
El cambio que experimenta el momento lineal de un cuerpo es proporcional a la fuerza resultante de todas las fuerzas que actúan sobre él y actúa en la dirección de esta.
Matemáticamente:
A partir de esta relación se deduce lo que actualmente conocemos con el nombre teorema del impulso y la cantidad de movimiento (momentum lineal).
domingo, 18 de abril de 2010
Teorema de Lamy



De esto se deduce el siguiente lema:
PROBLEMA
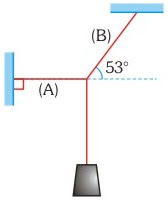
Si el sistema mostrado en la figura se encuentra en equilibrio estático en la forma que se indica, y el bloque P pesa 21 N, determinar el peso del bloque Q.
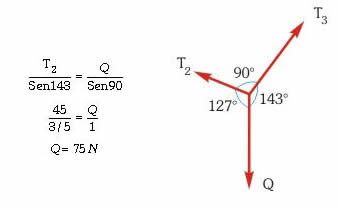
Hagamos el DCL del nudo A, teniendo presente que la tensión de la cuerda que sostiene el bloque P es igual a su peso, y apliquemos el teorema de Lami:

Equilibrio Mecánico
Se dice que un cuerpo se encuentra en equilibrio mecánico, cuando su estado de movimiento como conjunto no cambia en el tiempo. Este concepto es relativo porque el estado de movimiento de un cuerpo depende del sistema de referencia elegido.
Se distingue dos clases de equilibrio: traslacional y rotacional.
Se dice que un cuerpo se encuentra en equilibrio traslacional, respecto de cierto sistema de referencia, cuando su centro de masas se encuentra en reposo o se mueve con velocidad constante (movimiento rectilíneo uniforme) respecto de él.

Se dice que un cuerpo se encuentra en equilibrio rotacional, respecto de cierto sistema de referencia, cuando este no rota o se encuentra rotando con una velocidad angular constante (movimiento rotacional uniforme), respecto de él.

Si un cuerpo se encuentra en reposo, respecto de cierto sistema de referencia, se dice que el cuerpo se encuentra en equilibrio estático, que es la forma más común de equilibrio mecánico.
Por otro lado, existen tres formas de equilibrio estático: estable, inestable e indiferente.
Se dice que un cuerpo se encuentra en equilibrio estable si cuando un agente externo lo aleja ligeramente de su estado de equilibrio original, y lo deja en libertad de movimiento, este retorna inmediatamente a su posición original. En cambio, si este se aleja aún mas de su posición original, se dice que el cuepor se encuentra en equilibrio inestable.

Finalmente, se dice que un cuerpo se encuentra en equilibrio indiferente si cuando un agente externo lo aleja ligeramente de su estado de equilibrio original, y lo deja en libertad de movimiento, este no presenta tendencia ni a retornar a su posición original ni a alejarse aún más de esta.
Primera condición de equilibrio
Un cuerpo se encuentra en equilibrio de traslación, si la fuerza resultante de todas las fuerzas externas que actúan sobre él es nulo.
Matemáticamente:
Para el caso de fuerzas coplanares que se encuentran en el plano cartesiano xy se reduce la fuerza resultante en cada uno de los ejes x e y es cero:

Geométricamente esto implica que estas fuerzas, al ser gráficadas una a continuación de la otra, de modo tal que el extremo de cada una coincida con el origen de otra, formen un polígono cerrado.

Para el caso particular que sobre el cuerpo actúan solo tres fuerzas, estas deben formar un triángulo de fuerzas.

PROBLEMA
El bloque mostrado tiene una masa m = 5 kg y se encuentra en equilibrio. Si el resorte (K = 20 N/cm) se encuentra estirado 4 cm, determinar la tensión de la cuerda vertical.
Como K = 20 N/cm, cuya interpretación es que por cada centímetro de deformación del resorte la fuerza elástica que se genera internamente es de 20 N, se deduce (ley de Hooke) que cuando la deformación sea de 4 cm la fuerza elástica en el resorte será de 80 N.
Hagamos DCL del bloque, teniendo presente que tanto el resorte como la cuerda vertical se encuentran "tensadas" y por tanto las fuerzas que actúan sobre el bloque debido a estos cuerpos se grafican "saliendo" del bloque, y apliquemos la 1ra condición de equilibrio.

PROBLEMA
Si el bloque mostrado en las figura pesa 120 N, determinar las tensiones de las cuerdas A y B.
Como sobre el bloque solo actúan dos fuerzas (la fuerza de la gravedad y la tensión de la cuerda vertical) y este se encuentra en equilibrio, la tensión de la cuerda será igual (en módulo) a la fuerza de la gravedad del bloque.
A continuación hagamos DCL del nudo en donde convergen las tres cuerdas, teniendo presente que las tensiones de las tres cuerdas "salen" del nudo, y a continuación construyamos el triángulo de fuerzas.

Lo que a continuación se tiene que hacer es resolver, el triángulo de fuerzas construido. En este caso, relacionando el triángulo de fuerzas con el triángulo notable de 37° y 53°, deducimos que (k = 30).

PROBLEMA
Si la esfera mostrada en la figura es de 20N, y el módulo de la fuerza F aplicada es de 80 N, determinar los módulos de las reacciones del apoyo en A y B.
Hagamos DCL de la esfera teniendo presente que las reacciones del apoyo en A y B son perpendiculares a las superficies en contacto y se grafican "entrando" al cuerpo que se analiza.

Teniendo presente que los ángulos de la dos perpendiculares son iguales, deducimos que la reacción del apoyo en A (RA) forma con la vertical un ángulo que es igual al ángulo diedro 2θ.
Por otro lado, tenido presente que los ángulos alternos internos entre rectas paralelas son iguales, deducimos que la fuerza F forma con la horizontal un ángulo θ.
A continuación construyamos el triángulo de fuerzas tenido presente que la resultante de la reacción del apoyo en B y el peso apunta hacia arriba.

Se comprueba que el triángulo de fuerzas es un triángulo equilátero y por tanto:

jueves, 8 de abril de 2010
Naturaleza dual de la materia
En el siglo XVII se desarrollaron dos teorías contrapuestas sobre la naturaleza de la luz: una de parte el genial científico inglés Isaac Newton (teoría corpuscular) y por otra del matemático geómetra holandés Cristian Huygens (teoría ondulatoria).
Para Newton la luz estaba formada por pequeñísimos corpúsculos o partículas, y demostró las leyes de la reflexión y la refracción, en base a esa teoría. La luz se reflejaría como lo puede hacer una pelota cuando rebota sobre una superficie, y se refractaría al pasar de un medio a otro por la diferencia de velocidad de transmisión en los dos medios, pero no explicaba otros fenómenos como por ejemplo la difracción.
Debido al gran prestigio académico de Newton, la teoría de Huygens quedo relegada por más de un siglo, hasta que los experimentos de Thomas Young y Auguste Jean Fresnel la corroboraron ya en el siglo XIX.
Ver experimento de Tomas Young
Este experimento que demostró la naturaleza ondulatoria de la luz permitió, un siglo después, corroborar la doble naturaleza ondulatoria-corpuscular de todas las partículas. Contra toda lógica se ha observado que los electrones, los protones o cualquier partícula de materia goza también de una naturaleza ondulatoria. Haciéndo pasar a través de las dos rendijas haces de partículas se observan, también, patrones de interferencia tal como supuso en su día el físico francés Louis-Victor de Broglie.
Ver interferencia de electrones
Actualmente se considera que la dualidad onda-partícula es un “concepto de la mecánica cuántica según el cual no hay diferencias fundamentales entre partículas y ondas: las partículas pueden comportarse como ondas y viceversa”. (Stephen Hawking, 2001)
Simulacros de Admisión UNI
Etiquetas
Websites amigos
-
Gaussianos alcanza la mayoría de edad: ¡cumplimos 18 años! (y hay sorpresa) - Llegó el día en el que Gaussianos alcanza la mayoría de edad: cumplimos 18 años online. Desde aquel 26 de julio de 2006, en el que comenzamos hablando de l...Hace 16 horas
-
Italia: microplásticos en el semen en 6 de cada 10 hombres - *El tamaño de las partículas es ínfimo y de plásticos muy comunes, como polietileno y acrílico.* Se detectaron* trazas de micropartículas de plástico en 6...Hace 1 año
-
Si la realidad es determinista, eso significa que el libre albedrío es solo una ilusión cognitiva - [image: Si la realidad es determinista, eso significa que el libre albedrío es solo una ilusión cognitiva] Ya lo decía *Rudy Rucker*, matemático y precu...Hace 2 años
-
-
-
Material CEPREUNI
Libros para descargar
- Introducción a la Ciencia
- Química para todos (edit. MIR)
- Cuerpos físicos (edit. MIR)
- Moléculas (edit. MIR)
- Electrones (edit. MIR)
- Fotones y núcleos (edit. MIR)
- Geometría Recreativa
- La física del futuro
- Siete breves lecciones de física
- Los Grandes Matemáticos
- Qué es cálculo diferencial
- Las ecuaciones de Maxwell
- La clave secreta del universo
- LA FÍSICA aventura del pensamiento
- ¿Está Ud. de Broma Sr. Feynman?
- El Enigma de Fermat
- Crónicas de ciencia improbable
- 50 cosas que hay que saber sobre física
- El jardin de Newton
- ¿Sabe Usted Física
- Biografía de la Física
- Historia de las matemáticas
- Los Simpson y las matematicas
- Historia de la Física
- Todo es cuestión de química
- Geoquímica Recreativa
- La matemática de Pitágoras a Newton
- El sistema periódico
- Materia - Colección Life
- Einstein
- Una breve historia de casi todo
Archivo del blog
Seguidores
Tablón de Mensajes
Estadísticas