Dentro de ls múltiples usos que se le puede dar a la energía nuclear producida mediante la fusión o fisión de un átomo existe la posibilidad de generar energía eléctrica. El calor generado en las cualquiera de estas reacciones se utiliza para crear vapor de agua calentándola por medio de unas barras de metal que estan en contacto con material radioactivo. Éste vapor de agua, con su alta presión acciona las turbinas que, éstas si, són las encargadas de generar electricidad. El sistema seria parecido al de una central térmica.
Las turbinas están conectadas a un generador eléctrico. Uno puede imaginarse, salvando las distáncias, a la dinamo de una bicicleta. Lamentablemente no se puede aprovechar toda la energía y una gran cantidad de ella se pierde mediante calor o mediante la resisténcia de los materiales conductores.
Durante la fisión, los neutrones separados chocan contra otros átomos y van generando fisiones en cadena. Una de las dificultades es controlar este proceso puesto que de otro modo se acabaria provocando una grave explosión. Para ello, se colocan unas barras de control (generalmente són de carburo de boro) con el objectivo de absorver los neutrones libres, que de este modo no pueden provocar más fisiones. Si se colocan muchas barras de control se absorven todos los neutrones y se para el reactor.
Funcionamiento
El principio básico de una central nuclear és utilizar el calor producido en la fisión nuclear para calentar agua hasta convertirla en vapor a alta temperatura i presión. El vapor, llega hasta una gran turbina que hace girar. La turbina está conectada a un generador que cenvertirá el movimiento circular en energía eléctrica.
El encargado de calentar y transformar el agua en vapor és el reactor nuclear que se encuentra dentro de un edificio llamado edificio de contención. En el reactor nuclear se produce la fisión del núcleo de los átomos. Ésta és una reacción que genera gran cantidad de calor que se aprovecha para calentar el agua mediante elementos con alta conductividad térmica.
El agua transformada en vapor a alta temperatura sale del edificio de contención debido a la altra presión a la que está sometido hasta llegar a la turbina y hacerla girar. En este momento parte de la energía calorífica del vapor se transforma en energía cinética. Ésta turbina está conectada a un generador eléctrico mediante el cual podrá transformar la energía cinética enenergía eléctrica.
Por otra parte, el vapor de agua que salió de la turbina, aunque ha perdido energía calorífica sigue estando en estado gas y muy caliente, por lo que hay que refrigerarlo antes de volverlo a meter en el circuito. Por este motivo, que al salir de la turbina se dirige a un depósito de condensación donde estará en contacto térmico con unas tuberias de agua fría. El vapor de agua se vuelve líquido y mediante una bomba se manda de nuevo al reactor nuclear para volver a repetir el ciclo.



























 En este caso el móvil se mueve horizontalmente describiendo un MRUV en donde en cada segundo el módulo de su velocidad aumenta en 2 m/s. De esto se concluye que el módulo de su aceleración a es de 2 metros por segundo cuadrado (2 m/s2).
En este caso el móvil se mueve horizontalmente describiendo un MRUV en donde en cada segundo el módulo de su velocidad aumenta en 2 m/s. De esto se concluye que el módulo de su aceleración a es de 2 metros por segundo cuadrado (2 m/s2).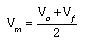




 En este caso el móvil se mueve horizontalmente describiendo un MRU recorriendo una distancia de 3 metros en cada segundo de tiempo. De esto se concluye que la rapidez constante con que se mueve el móvil es de 3 metros por segundo, es decir el módulo de su velocidad V es de 3 m/s.
En este caso el móvil se mueve horizontalmente describiendo un MRU recorriendo una distancia de 3 metros en cada segundo de tiempo. De esto se concluye que la rapidez constante con que se mueve el móvil es de 3 metros por segundo, es decir el módulo de su velocidad V es de 3 m/s.


















