Problema de Física: Relación de velocidades angulares

Hace algunos meses un alumno me dio este problema (creo que era de la Vallejo) que me pareció interesante.

PROBLEMA
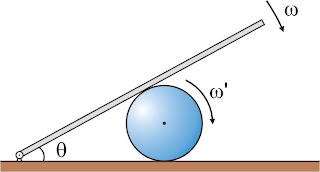
Una plataforma rota lentamente alrededor de un eje que pasa por uno de sus extremos con una velocidad angular constante ω y hace rodar un cilindro apoyado en una superficie horizontal áspera. Si consideramos que la esfera rueda sin resbalar en la supercifie horizontal y resbala respecto de la plataforma, determinar la velocidad angular ω' del cilindro cuando la barra forma un ángulo θ respecto de la horizontal.

Debido a que la resolución de este problema es ilustrativo para alumnos y docentes paso a mostrarles su resolución.

Se denomina centro instantaneo de rotación (CIR) de un cuerpo rígido, que se encuentra en movimiento en un cierto plano, a un punto de dicho plano que puede considarse como si en ese instante dicho cuerpo se encuentra efectuando un movimiento de rotación pura alrededor de él.

Si el cuerpo realiza una rotación pura alrededor de un punto, dicho punto es el CIR.

Si el cuerpo realiza un traslación pura el CIR se encuentra en el infinito en dirección normal a la velocidad de traslación.

Si el cuerpo realiza un movimiento general el CIR se mueve respecto al cuerpo de un instante a otro (de ahí que se llame centro instantáneo de rotación). Su posición se puede conocer en cada instante por intersección de las direcciones perpendiculares a la velocidad de dos de sus puntos.

Cuando un cilindro rueda sobre una superficie sin resbalar el CIR es el punto de contacto con dicha superficie.

En este caso el módulo de la velocidad de cada uno de los puntos del cilindro es igual al producto de su velocidad angular multiplicada por su distancia al CIR (punto O) y su dirección es perpendicular al segmento que une dicho punto con el CIR. En este problema, la rapidez del punto del cilindro en contacto con la plataforma será ω' r' = ω' (2 R cos θ/2).

Por otro lado el módulo de la velocidad de cada uno de los puntos de la plataforma es igual al producto de su velocidad angular por su distancia al eje de rotación y su dirección es perpendicular a la plataforma. En este problema, la rapidez del punto de la plataforma en contacto con el cilindro será ω r = ω(R cot θ/2).

Pero la velocidad absoluta del punto del cilindro en contacto con la plataforma (ω' r') resulta de la composición de su velocidad relativa a la plataforma (v_rel) con la velocidad de arrastre de la plataforma (ω r).

Del triángulo mostrado se deduce que ω' r' sen θ/2 = ω r: