Hace unas horas mi colega Oswaldo Farro propuso un problema de Física en el face, que fue propuesto en un examen selectivo regional en la Olimpiada Rusa.
El problema es el siguiente:
PROBLEMA
En un cilindro de radio R se coloca un tabla de longitud 2L y masa despreciable, en cuyos extremos se han fijado dos esferillas de masa m cada una. Determinar el periodo de las pequeñas oscilaciones del sistema.
Resolución
Primero debemos señalar que cuando el sistema formado por la tabla y las esferillas oscila, siempre hay un torque recuperador que lo regresa a la posición a la posición horizontal, esto es, a la posición en donde la tabla si es que estuviera en reposo estaría en equilibrio. A partir de ahora nos referiremos a este sistema físico simplemente como "sistema".

Para oscilaciones pequeñas, este movimiento oscilatorio es análogo a un movimiento armónico simple (MAS) en donde hay una fuerza recuperadora FR que es proporcional a la distancia de alejamiento x de la posición de equilibrio (FR = - kx). El sigo negativo en esta relación es debido a que siempre la fuerza recuperadora FR tiene dirección opuesta al desplazamiento x del cuerpo que oscila respecto de la posición central, como claramente se visualiza en la siguiente animación.
A manera de ilustración, recordemos como se determina el período de oscilación T de un MAS.
Para esto se expresa la fuerza recuperadora FR en función de la masa m que oscila, frecuencia angular ω y de la distancia de alejamiento x (para debemos tener en cuenta la 2da ley de Newton y recordar que la aceleración del MAS es -ω2x), se reemplaza en la expresión FR = - Kx, y en esta ecuación se elimina la distancia x .

De aqui recordando que la frecuencia angular ω es igual a 2π/T, se concluye que:

En este caso se debe proceder de manera análoga, pero considerando conceptos de dinámica rotacional, como momento de inercia y la relación torque-aceleración angular.
Bueno, alli vamos.
Como se entiende que la barra rueda sin resbalar sobre el cilindro se cumple la siguiente relación geométrica.

Hagamos DLC del sistema y apliquemos la relación torque-aceleración angular, respecto del punto P.
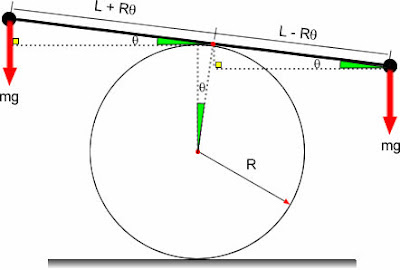

A partir de esto, y considerando que para ángulos θ (en radianes) pequeños el producto Rθ es también despreciable y la función coseno es prácticamente 1, se deduce que:

Pero asumiento que este movimiento rotacional oscilatorio es análogo al MAS, debemos suponer que también en este caso la aceleración (angular) es proporcional al alejamiento (ángular) de su posición de equilñibrio, es decir:

Reempalzando esto en la relación anterior se deduce que:




0 comentarios:
Publicar un comentario